Grandes Géodésiques:
Commentaires introductifs
En premier lieu, qu'entend-on par "géodésique"?
C'est une courbe sur une surface qui minimise l'énergie sur son trajet, par exemple une ligne droite dans le plan. Pour ce qui nous concerne ici, il s'agit du plus court chemin entre deux points sur un ellipsoïde de révolution. En navigation, le terme utilisé est celui "d'orthodromie", bien que généralement relatif à un modèle de Terre sphérique.
Si, pour la sphère, la détermination d'une géodésique-orthodromie s'effectue à l'aide de formules relativement simples de trigonométrie sphérique, il n'en est pas de même pour l'ellipsoïde, où il est fait appel à des intégrations complexes.
Les problèmes à résoudre: problème direct, problème inverse
1/ problème direct :
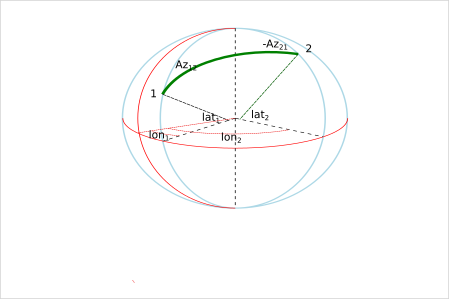
Soit un point de départ de longitude et latitude données, à partir duquel selon un azimut donné on effectue une trajectoire géodésique sur une distance donnée. Quelle est alors la position en longitude / latitude du point d'arrivée, et accessoirement son azimut inverse.
2/ problème inverse :
Ici, on se donne deux points (l'un de départ, l'autre d'arrivée), et l'on désire connaître la distance (la plus courte!) qui les sépare, ainsi que les azimuts aller et retour. C'est le cas le plus fréquent d'utilisation des calculs proposés ici.
Ce qui est proposé ici
On trouvera dans les onglets suivants de quoi résoudre les deux problèmes, soit par saisie numérique pure (onglet Direct/Inverse), soit de manière plus graphique et moins austère dans l'onglet "Visualisation" (problème inverse seulement).
Un dernier onglet permet de garder trace des calculs effectués.
Grandes Géodésiques:
problème direct / problème inverse
Ellipsoïde a= m b=m f=1/
digits geo az dis
Départ (point n°1):
londd1 latdd1 azdd12 dis12
Arrivée (point n°2):
londd2 latdd2 azdd21 dis21
Direct
Inverse run
Visualisation
Votre géodésique facile en trois clicks sur la carte ci-dessous : Point de départ : simple click Point d'arrivée : double click, puis bouton calcul?
P
Réalisé par AH,
Webmaster du site http://ahgeodev.fr/
Stockage des résultats
dernier résultat